Ben's fusion reactor design

Introduction

This is a quick summary of my work to date on a novel design of nuclear fusion reactor.

I've been looking into a method of confinement that uses static electricity and avoids expensive magnets or lasers. I was initially inspired in part by Daniel Knapp's electrostatic trap [1], but on playing around with a few alternative designs decided that a Kingdon trap [2] would probably form a better basis for a reactor.

The Design

The reactor has a cylindrical shape and contains a vacuum. A rod-shaped electrode runs down the central cylindrical axis of the reactor - forming a kind of spindle. For initial purposes imagine it to be 2m long with a radius of 1m. A large negative static electric charge is placed on the central electrode. Positive ions are injected into the reactor so that they fall into an orbit around the electrode. The details of the injection method will not be considered here. An individual ion traces out a path such as that illustrated in Figures 1 and 2.

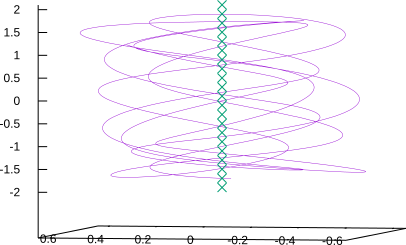
The ion pictured in these diagrams is contained radially by being in orbit around the electrode. It is contained in the cylindrical (or z) direction by being attracted to the mid-point of the rod, where the electric field is strongest.

All the ions are inserted so they orbit the electrode in the same direction. If ions were inserted in both orbital directions then the subsequent collisions would cause them to loose their forward momentum and they would tend to fall towards the central electrode.

For fusion to occur ions must collide. Ions may collide as they traverse the z dimension in opposite directions, or radially as a result of following rosetta-shaped orbits.

To be most effective the ions should be all of the same type, with pure deuterium or pure helium-3 being the most likely candidate fuels.

Issue 1 - Containment / Ion scattering

This quality of the containment is the first of (at least) two major issues that need to be considered.

Most ion collisions don't result in fusion, and after a collision the velocity of both particles change. Thus after a collision there is a risk of an ion escaping orbit, hitting the central electrode, or else escaping along the cylindrical (z) axis.

I performed many simulations to see how often particles would escape, and it turned out that escapes were surprisingly rare. Perhaps it should not have been so surprising as both of the ions in a collision initially have enough forward momentum to stay in orbit and this forward momentum is preserved throughout the collision. In addition there is probably also a tendency for ions to move back towards the mean orbital radius and mean energy level as the paths of the less energetic "inner" ions cross those of the more energetic "outer" ions and when the two types collide an averaging of speed and energy occurs. Note that the behaviour of ions on the outer edge of the plasma is difficult to model due to the diffuseness of the plasma in this region, so the simulations are not conclusive regarding containment.

These simulations have indicated that it is possible to produce more energy in fusion than is lost due to scattering, which is an exciting finding. Quantum tunnelling was factored into the simulations, but losses due to Bremsstrahlung radiation and cyclotron radiation were not.

It was assumed that the charge on the electrode was a good deal larger than the plasma charge so the effects of the electric and magnetic fields of the plasma could be ignored.